สมการกำลังสาม

ตัวอย่างกราฟของสมการกำลังสาม

ในทางคณิตศาสตร์ สมการกำลังสาม คือสมการของพหุนามตัวแปรเดียวที่มีดีกรีเท่ากับ 3 รูปแบบทั่วไปของสมการกำลังสามคือ

$ax^3 + bx^2 + cx + d = 0 \!$

เมื่อ a ≠ 0 (ถ้า a = 0 สมการนี้จะกลายเป็นสมการกำลังสอง) โดยปกติแล้ว

a, b, c, d

คือสัมประสิทธิ์ที่เป็นจำนวนจริง ฟังก์ชันของสมการกำลังสามสามารถวาดกราฟบนระบบพิกัดคาร์ทีเซียนได้รูปเส้นโค้งคล้ายตัว S หรือ N

ดิสคริมิแนนต์

สมการกำลังสามทุกสมการที่มีสัมประสิทธิ์เป็นจำนวนจริง จะมีรากของสมการ 3 คำตอบเสมอ ซึ่งจะต้องมีจำนวนจริงอย่างน้อยหนึ่งจำนวนที่เป็นคำตอบ ตามทฤษฎีบทค่าระหว่างกลาง (intermediate value theorem) และคำตอบเหล่านั้นอาจจะเท่ากันบางค่าก็ได้ ส่วนอีกสองจำนวนที่เหลือสามารถแยกแยะได้จากการพิจารณาดิสคริมิแนนต์ ซึ่งคำนวณจาก

$\Delta = 4b^3d - b^2c^2 + 4ac^3 - 18abcd + 27a^2d^2 \!$

คำตอบของสมการจะเป็นประเภทใดประเภทหนึ่ง ดังต่อไปนี้

ถ้า Δ < 0 คำตอบของสมการจะเป็นจำนวนจริงทั้งสามค่า ที่แตกต่างกันทั้งหมด
ถ้า Δ > 0 คำตอบของสมการจะมีหนึ่งค่าที่เป็นจำนวนจริง และอีกสองจำนวนเป็นจำนวนเชิงซ้อนสังยุคซึ่งกันและกัน
ถ้า Δ = 0 คำตอบของสมการจะเป็นจำนวนจริงทั้งสามค่า ซึ่งมีสองจำนวนเป็นค่าเดียวกัน หรือ เป็นค่าเดียวกันทั้งสามจำนวน อย่างใดอย่างหนึ่ง

สูตรกำลังสาม

ถ้าหาก

x 1, x 2, x 3

เป็นคำตอบของสมการกำลังสามแล้ว เราจะสามารถแยกตัวประกอบของพหุนามกำลังสามได้ดังนี้

$ax^3 + bx^2 + cx + d = a(x - x_1)(x - x_2)(x - x_3) = 0 \!$

กำหนดให้

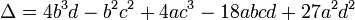
$\begin{align} q &= \frac{9abc - 27a^2d - 2b^3}{54a^3} \\ r &= \sqrt{\left (\frac{3ac-b^2}{9a^2}\right )^3 + q^2} \\ s &= \sqrt[3]{q + r} \\ t &= \sqrt[3]{q - r} \\ \end{align}$

คำตอบของสมการทั้งสามค่าสามารถคำนวณได้จากสูตร

$\begin{align} x_1 &= s+t-\frac{b}{3a} \\ x_2 &= -\frac{1}{2}(s+t)-\frac{b}{3a}+\frac{\sqrt{3}}{2}(s-t)i \\ x_3 &= -\frac{1}{2}(s+t)-\frac{b}{3a}-\frac{\sqrt{3}}{2}(s-t)i \\ \end{align}$

เมื่อ i คือหน่วยจินตภาพที่นิยามโดย i² = −1

ที่มาจาก http://th.wikipedia.org/wiki/%E0%B8%AA%E0%B8%A1%E0%B8%81%E0%B8%B2%E0%B8%A3%E0%B8%81%E0%B8%B3%E0%B8%A5%E0%B8%B1%E0%B8%87%E0%B8%AA%E0%B8%B2%E0%B8%A1

chamina

วันอังคารที่ 10 มกราคม พ.ศ. 2555